Hi everyone,
“The Big Chill” series seems to have been quite well received, and I thank you all for your comments and feedback. I’m turning now to the question of inference. As many of you know it’s a core theme in my book, The Myth of Artificial Intelligence, and I think it shines a bright light on why LLMs, while impressive in many cases, are quite far from a candidate for AGI. I’ll jump in on this one after a brief summary of the “inference framework” I discussed in the Myth. I hope you enjoy, and thanks again. We hit 1,000 subscribers (and many more followers), and I’m really grateful. As always, if you find Colligo helpful please do consider a paid subscription.
If It Walks Like a Duck
Inference in the technical mathematical or computational (or philosophical) sense is simply the question of what’s reasonable to conclude given some prior knowledge and some current observation—given what you know and what you currently see. If I see a duck crossing the road, I might conclude it’s in fact an armadillo cleverly disguised as a duck, dressed up by some merry pranksters, or I might think it’s an alien lifeform that looks remarkably like a duck but in fact carries a ray gun, or I might think it’s a, well, a duck. Inference is what’s reasonable to conclude given what I see in front of me and what I already believe. Lacking any evidence to the contrary, and knowing that ducks sometimes waddle across roads, and “duck” is an animal that in fact lives on planet Earth, it’s reasonable to conclude seeing a duck-like thing waddle across a road that it’s a duck. (If it walks like a duck, and quacks like a duck….).
In the annals of science, smart folks would sometimes refer to these inferences as inductions, because (unlike with a deduction about something) there’s no necessary reason for a duck-like thing to actually be a duck. We don’t deduce that we see a duck crossing the road, like we might deduce that a triangle has three sides, or that Socrates is mortal because he’s a man and men are mortal (this is a famous example of a deductive syllogism known as modus ponens). We see lots of waddling feathered waterbirds that are described in English as “a duck,” and by provision of many examples of ducks we infer the next one we see: it’s a duck. This is induction because it’s by examples (data) that we gain knowledge of the world. Deduction is different. Armed with Euclid’s geometry, I can see one triangle and deduce (not induce) all sorts of properties about it. I don’t need to see millions of triangles. There’s no geometry of ducks—we look at many examples of them and notice what they all have in common. We don’t deduce their properties from first principles.
What do they have in common?
Of Swans and Triangles
Induction has been extensively developed in science and the philosophy of science as well as mathematics, and it can get complicated and mathematically difficult. But at root, it’s enumerative. It’s, yes, counting. To take the classic example, if we see a thousand swans and they all are white, we might conclude by induction that “All swans are white.”
Are the rest of you white?
It’s the counting up of examples from observation that gives power to induction. It’s also this basic enumerative scheme that accounts for its obvious weakness: perhaps the next observation is of a black swan? What then? It takes one counterexample to invalidate a general rule inferred inductively. We call this type of inference ampliative, because it adds knowledge, but also not necessary, because it can always be wrong—just around the corner. A triangle can’t stop having three sides.
I can’t stop having three sides.
Humans use induction and deduction all the time. We also use a third type of inference that has received various labels over the years but in its formulation by the polymath American scientist, mathematician, and logician Charles Sanders Peirce, it goes by abduction (or “retroduction,” but most scholars settled with “abduction”). Abduction, like induction, is a “weak” form of inference because it can be wrong—it’s not necessary that the conclusion follows given the premises—and it’s also ampliative, in the sense that we gain new knowledge of the world and don’t just churn through definitions, as with deduction.
Abduction is sometimes referred to as “inference to the best explanation,” because it’s essentially a guess about an observation—why did such-and-such happen? Peirce called it a “surprising observation,” that would be a matter of course if something else were true. Thus is fancy language for pointing out that we use background knowledge to piece together a constantly moving and updating picture of the world. If I walk into the kitchen and there’s a half empty can of Coke sitting on the counter, I might conclude it’s from the workmen who were in the house earlier repairing the sink. Or perhaps it was my sister, who loves Coke and has a habit of dropping by unannounced, beverage in hand. These aren’t inductions, because I’m not thinking that I’ve seen a thousand example of cans of Coke in similar circumstances (what would that even mean?), or that I can deduce—not in the Sherlock Holmes sense, those were abductions!—how and why the can of coke is sitting on the counter. They’re guesses—abductions—which are plausible explanations given what I already know. Frequency may play a role, but it’s not intrinsic to the inference, and in fact abductions are notorious for being most interesting when they have the fewest prior (known) examples, as with scientific discovery and invention. (Big, big point that I will develop more in a later post.)
We’re constantly performing abductions—they’re like a condition of us being alive at all. In the book I pointed this out, and I pointed out that since computers or AI systems weren’t technically doing abductions, they couldn’t be candidates for human-like thinking. The AI systems of today are all machine learning systems. Machine learning isn’t really “learning,” it’s better described as providing a bunch of examples (or data) to an optimizing function, and generating a “rule” or model for predicting (or classifying) new, unseen examples. Here, the details actually don’t matter much. What matters is that the type of inference performed by AI systems using machine learning is broadly inductive. Data is our prior examples. And “big data” is lots of prior examples, like observing a million swans of color white or a million waddling waterbirds looking like Mallards. And here’s the question: if induction is so weak and hopeless as a form of commonsense inference, why do LLMs (seemingly) work so well? Well. Why?
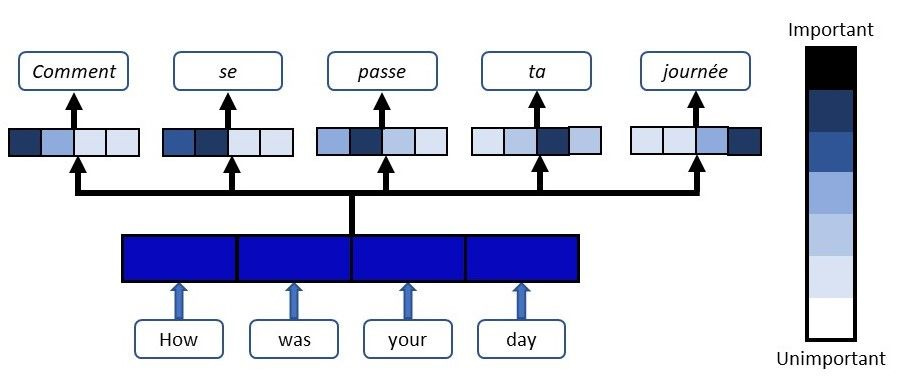
Here’s a Cliff Notes version of what LLMs are doing behind the scenes, by way of explaining how they’re actually quite limited even as they certainly have shown impressive performance. First, they use something called a “transformer architecture” with an “attention mechanism” to survey in essence entire sentences or prompts (sequences of tokens), rather than their predecessors, systems that would look a token or two behind, or in front, but always in a small window or context on a target token (the one currently under consideration). Transformers changed all this, by essentially capturing long range dependencies in language, so that “Though it wasn’t the case, several years of investigation and thousands of interviews led to the belief that Jones was in London.” Where was Jones? Before transformers, the systems would see a more limited context and (very likely) conclude he was in London. The dependent clause beginning the sentence wouldn’t get “seen.”
In addition, attention means that the relative importance of words (tokens) gets updated during training, so that the words in the sentence or prompt in effect “announce” their role in the overall meaning. In truth, it’s a clever and perhaps even brilliant innovation in natural language processing. It made possible much more powerful systems. And it’s still induction. And that means it can’t be AGI.
The best way to see the inherent limitations of the approach is to ruminate on the errors such systems make. The errors can sometimes be understandable blunders, but far too often make no sense, and show quite clearly that the system isn’t using an underlying, more flexible type of inference that would grant it “commonsense knowledge” about the world, or what we sometimes call a “world model.” This means, a model of what things actually mean in space and time, how things interact, how logic determines outcomes (I can’t both be in the store and driving home), and so on.
LLM “hallucinations” aren’t really even mistakes. They’re just gaps or blind spots in the inductive machinery that requires trillions of examples to compute relevance (this is called an embedding, though it’s a bit out of scope for this post, but not a future one). I once had an LLM—it was GPT-4, a quite powerful system—insist that “A” and “not-A” were both true. It saw no reason to retract this inference given the probability sequence that got it there. There was nothing but probability for generating the next most likely token, and if that meant that the duck was crossing the road and getting eaten by the farmer’s family for Thanksgiving at the same time, so be it. There’s no underlying inference that props up induction, it’s just big, big data. By contrast, abduction presupposes a world model, a set of background facts and rules that can be applied to observations. If there’s no world model to make use of, there’s no abduction. In other words, if LLMs really had abductive inference, they’d have an understanding of the world like we do, and their “hallucinations” wouldn’t look so mindless and bizarre. To put it another way, if LLMs weren’t so intrinsically tied to their training data, they might have a prayer of bringing commonsense or world knowledge to their inferences or responses.
Learning? Unfortunately, No. The Mistakes Will Keep Happening—there’s no “there, there.”
The takeaway is what I’ve referred to as “moving the needle” of what’s possible with very large inductive systems with powerful machine learning architectures like transformers. Many natural language processing tasks have seen significant increases in performance (accuracy) given this new approach. Unfortunately, it keeps us stuck in induction, and it pushes real AGI and real understanding in systems somewhere in our future, yet again. That future may never truly arrive—the science is, as always, never quite resolved. But we’re not there yet. We’re still stuck in fantastically complex, computationally expensive induction machines that can only infer based on the data provided to them. That’s not intelligence, even as it sometimes seems like it is.
In a future post I’ll take up some other issues regarding inference and LLMs, such as how embeddings work, and how tokens are actually generated. These details I hope will provide a richer picture of LLMs, but they won’t change the basics I’ve laid out here.
Erik J. Larson











Really enjoyed this. Don't know if this will contribute or not, but the problem I've always had with the Black Swan metaphor is that it's an academic exercise quite unrelated to the real world. If swans were the only thing ever seen, and they had always been white, it would be somewhat understandable, though foolish, for someone to lay down a law that "all swans are white" (and therefore - on Talib's thesis - a black swan represents something that "shocks the system.") But swans aren't "all there are." I've seen black dogs and white dogs, black horses and white horses, black sheep and white sheep, etc ... so upon seeing a lot of swans, I would never assume that they must all be white, no matter how many I'd seen and no matter how often they came up white because there is nothing like a mathematical proof that compels swans to be white. All we would know (as I think you point out) is they have all come up white - voice of Homer Simpson here - *so far ...*
(This, btw, is part of CS Lewis's critique of Hume's argument against the miraculous based on 'uniform human experience.' Even if human experience on this matter was uniform, it would be no proof against the miraculous and, btw, the experience is *hardly* uniform.)
So the appearance of even one black swan that immediately and irrevocably wrecks that 'law' is only "shocking" to the degree one sillily put one's confidence in a causal statement that wasn't logically compulsory. This would I think constitute another example of "us[ing] background knowledge to piece together a constantly moving and updating picture of the world."
Important stuff!
The questions that become salient now, of course, are these: What is it for an intelligence to "have a world-model"? And how does a world-model-having intelligence come to have that world-model?
Roughly, those who answer the first question along one dimension will answer the second by insisting we can program world-models, and those who answer the first question along a different dimension will answer the second by insisting world-models cannot be programmed. At those extremes, and in between them, much thinking has taken place and still needs to take place.
Looking forward to the upcoming posts!